こんにちは!出前館開発本部のロバートです。
現在、出向先の出前館で地理情報サービスの開発に携わっています。
出前館では、位置情報(例えば、緯度経度)を基に関連するデータを検索したい場面が多くあります。典型的な例としては、以下のようなものがあります:
- 配達先がある店舗の配達領域に含まれているかどうかを確認したい場合
- 特定の配達先に配送可能な店舗の一覧を取得したい場合
- 行政区画(例:都道府県や市区町村)ごとにGMVやドライバーのマッチ率などのKPIを統計したい場合
- この場合、配達先やドライバーの緯度経度を基に、その位置を包含する領域を調べる必要があります。
論理的には、行政区画などのポリゴン(多角形)データを持っていれば、上記のクエリを実現できます。しかし、実際に実装してみると、緯度経度に基づいてポリゴンをクエリする際に速度の問題がありました。そこで、高速な検索を実現するために、空間インデックスを導入することを決定し、H3という技術を採用しました。
本記事では、H3を用いてポリゴンを空間的にインデックス化する方法をいくつかご紹介したいと思います。
そもそもH3とは?
H3というのはUber社が開発した六角形に基づいた、オープンソースの空間インデックスです。
地理空間インデックスの一種で、地球を多数の六角形(セル)に分割する仕組みになっています。
- 正確に言うと、12個の五角形も入っているので、六角形の多いサッカーボールに近いイメージです。
- そして、16段階の解像度が提供されており、グリッドの細かさを調整できます。
各セルに識別子が付与されているため、インデックスとして利用可能です。
位置情報を持つデータをインデックス単位で集約するユースケースが一般的です。単なる位置情報(例:地点)の場合はその座標がどのセルに含まれているかを確認することで、H3インデックスを算出できます。アルゴリズムは比較的単純で、曖昧な部分がほとんどないため、把握しやすいです。
一方で、ポリゴン・多角形の場合はどのように対応すればいいでしょうか?座標と異なり、1つ以上のH3セルにマッピングするのが案外難しいです。
例えば、H3セルの中心点がポリゴンに包含されている場合、対象にしますか?
- それとも、H3セルが完全に包含されている場合のみを対象にしますか?
- あるいは、ポリゴンに交差しているH3セルをすべて対象にしますか?
H3や空間インデックスの文脈において、こういう「マッピング方法」は「インデックス方法」とも呼びます。
これから上記に登場したインデックス方法をそれぞれ説明します。
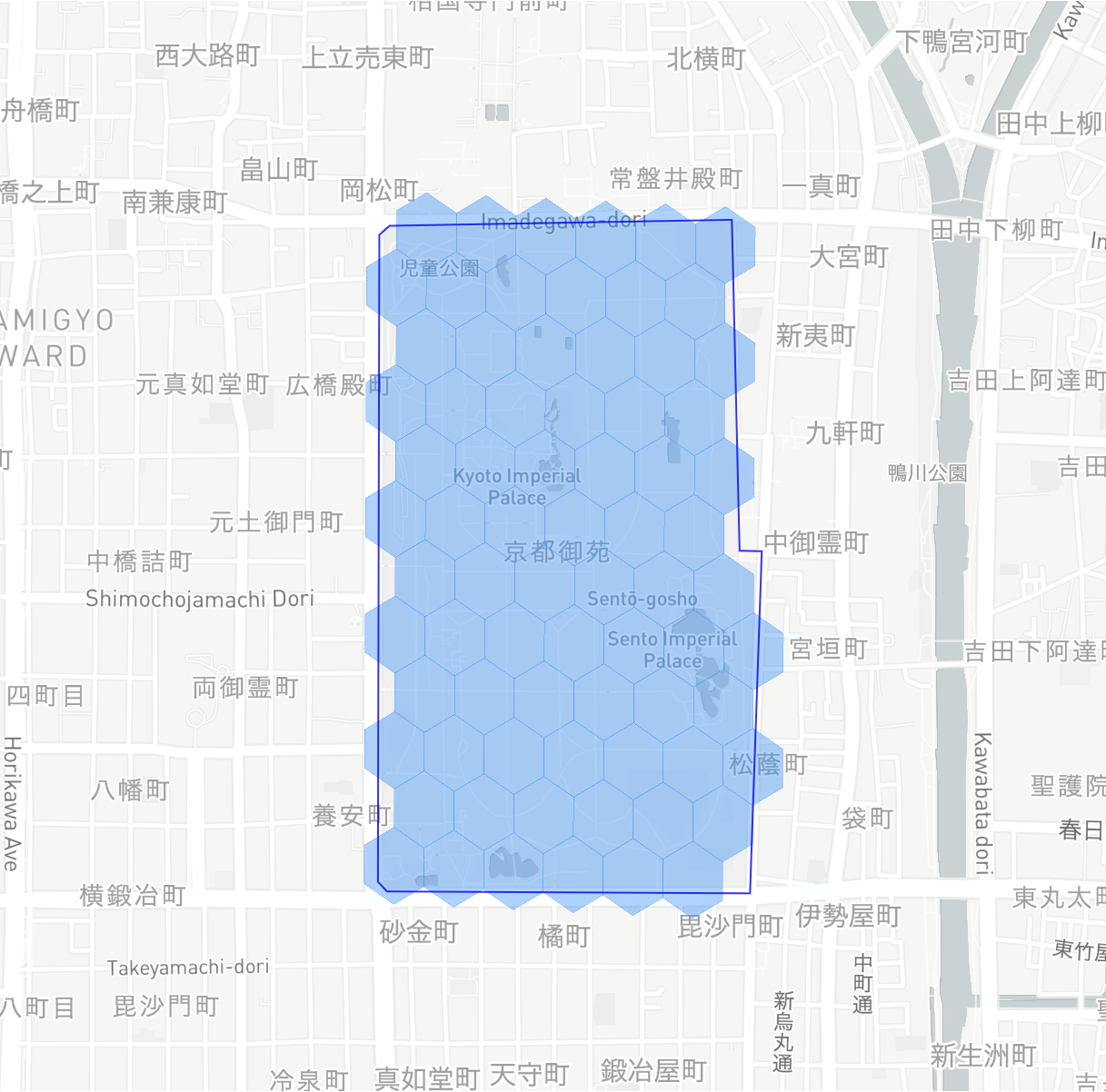
インデックス方法(1):中心点(Center Point)
H3の標準的なインデックス方法はセルの中心点を基にした方法です。
H3ライブラリには対応する関数が備わっており、デフォルトで使用されているため、ポリゴンにおいて「H3インデックス」と言えば、最初に思い浮かぶのはこの方法でしょう。
アルゴリズムは上記に述べた通り、わりと簡単です:
- H3セルの中心点がポリゴンの内側に入っていれば、対象にします。
結果は以下のようになります:
このインデックス方法には以下のメリットとデメリットがあります。
| メリット | デメリット |
|---|---|
| アルゴリズムが簡単で、処理が速い | H3セルがポリゴンに重なっていても対象外となる場合がある ・言い換えると、抜け穴・隙間ができてしまう |
| 標準的なアルゴリズムのため、追加開発が不要 | H3セルがポリゴンの境界線からはみ出る場合がある |
| 理解しやすい・説明しやすい |
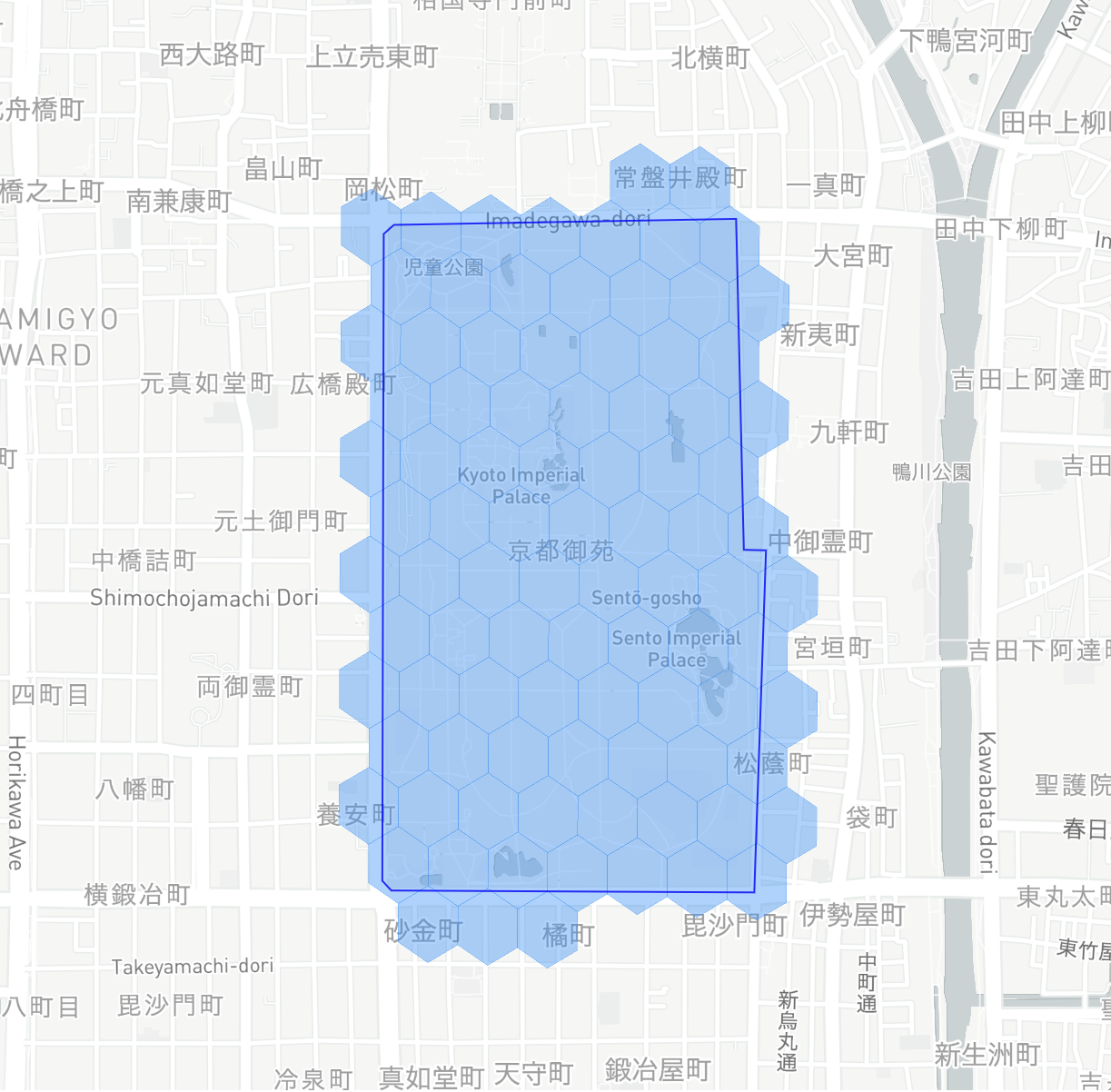
インデックス方法(2):交差(Intersection)
ポリゴンの境界線とH3セルの境界線が交差している場合、そのセルを対象にする方法です。
- 中心部分を省きたくないため、完全に包含されているセルも対象にします。
- つまり、H3セルが少しだけでもポリゴンに重なっていれば、対象となるということです。
H3ライブラリにはこのインデックス方法を実装する関数(polygonToCellsExperimental)があります。
- この機能は現時点ではexperimentalな機能として提供されています。
CONTAINMENT_OVERLAPPINGを渡すと、ここで話している交差のインデックス方法と同等の結果が得られます。
アルゴリズムは以下の通りです:
- まず、中心点に基づいたインデックス方法((1))を利用し、ベースとなるセルを算出します。
- このセルは全部結果セットに追加します。
- 各ベースセルについて:
- 既にチェック済みの場合はスキップします。
- 近隣のセルを算出し、ポリゴンの境界線に交差しているかどうかを確認します。
- gridDiskの関数を使用することで、近隣のセルを算出できます。
- 検索領域をどれだけ拡張するかはデータや要件によります。
- 交差している場合は結果セットに追加します。
結果は以下のようになります:
中心点アルゴリズムと比較すると、交差のアルゴリズムの方が複雑ですが、以下のメリット(とデメリット)があります。
| メリット | デメリット |
|---|---|
| 位置(緯度経度)がポリゴンの内側にあるけど、その位置を含むH3セルがポリゴンに該当しないケースが起きない | アルゴリズムがH3ライブラリに入っているが、最近追加された機能で、まだステーブルではない ・APIはまだ固まっていないので、変わる可能性がありそう |
| ポリゴンの空間インデックスとしてH3セルを使う場合はミス・漏れがない | 中心点のアルゴリズムと比べると、実装が複雑になる ・交差チェックの範囲をどこまで広げるか決める必要がある |
| 理解しやすい・説明しやすい | H3セルがポリゴンの境界線からはみ出るケースが発生する(ほぼ確実に) |
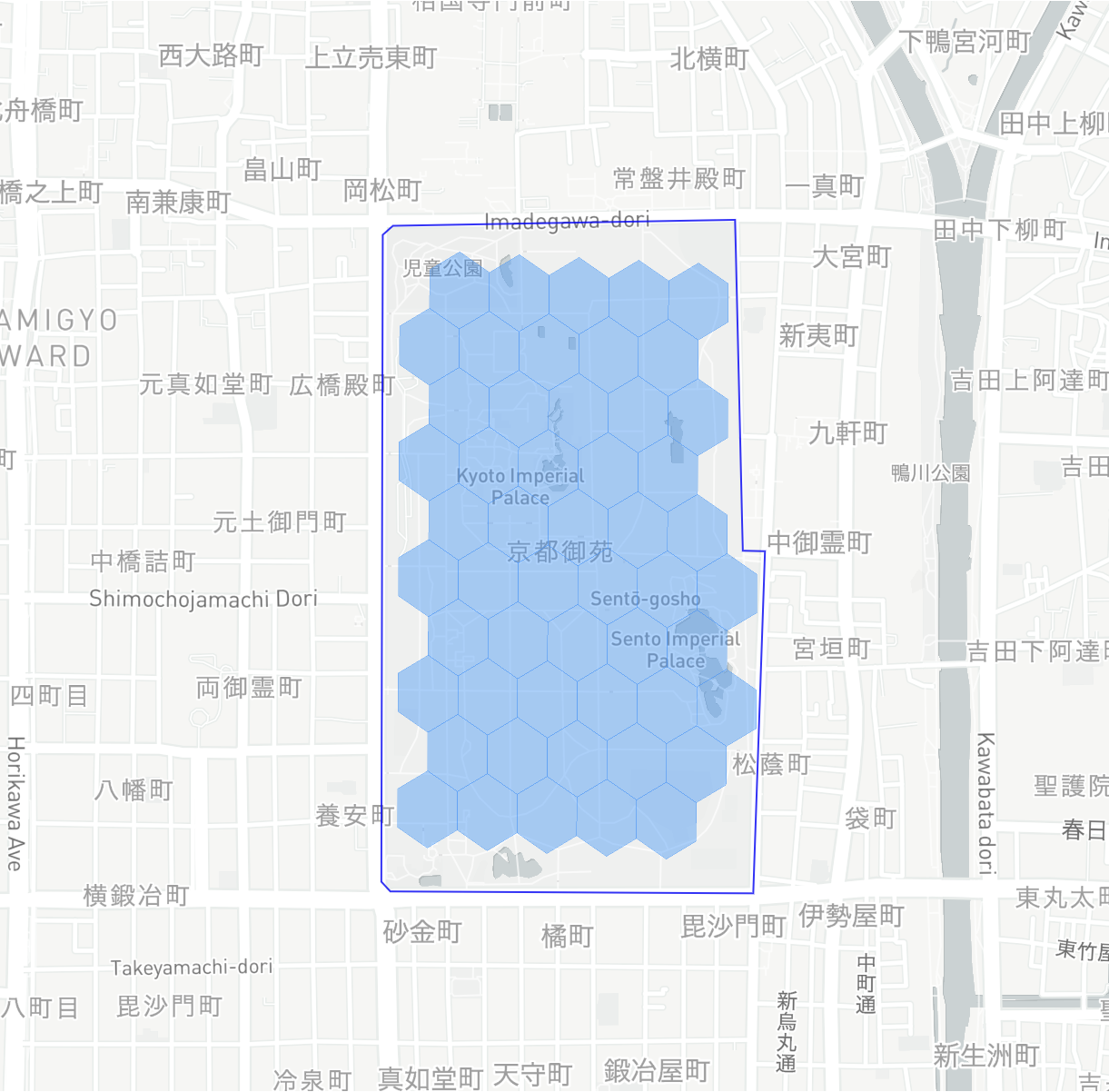
インデックス方法(3):包含(Containment)
H3セルがポリゴン内に完全に包含されている場合、そのセルを対象にする方法です。
- この方法の特徴は、H3セルがポリゴンの境界線からはみ出るケースが発生しないことです。
また、このインデックス方法を実装する関数がH3ライブラリに存在します:
- この機能も現時点ではexperimentalな機能として提供されています。
- polygonToCellsExperimentalに
CONTAINMENT_FULLを渡すと、ここで話している包含のインデックス方法と同等の結果が得られます。
アルゴリズムは以下の通りです:
- まず、中心点に基づいたインデックス方法((1))を利用し、ベースとなるセルを算出します。
- このセルはすべて結果セットに追加します。
- 各ベースセルについて:
- 既にチェック済みの場合はスキップします。
- ポリゴンの境界線に交差しているかどうかを確認します。
- 交差している場合は結果セットから削除します。
結果は以下のようになります:
| メリット | デメリット |
|---|---|
| H3セルがポリゴンの境界線からはみ出るケースが発生しない | ポリゴンがあまりにも小さい、あるいは解像度が粗い場合はポリゴンに完全に包含されているH3セルが存在しないため、どのH3セルでも適用されない可能性がある |
| アルゴリズムがH3ライブラリに入っているが、最近追加された機能で、まだステーブルではない ・APIはまだ固まっていないので、変わる可能性がありそう | |
| 中心点のアルゴリズムと比べると、実装が複雑になる |
どのインデックス方法を使えばいいの?
3つのインデックス方法を紹介しましたが、どれが一番いいでしょうか?
実は正解がないのです。
ニーズによって、最も適切な方式が変わるので、ユースケース次第です。
とはいえ、それぞれの方法には特徴があるため、特定のユースケースに対してどのインデックス方法が適しているかを整理できます。
典型的なユースケースを見てみましょう:
| ユースケース | インデックス方法 | 理由 |
|---|---|---|
| ポリゴンの形を表す | 中心点(Center Point) | 大抵の場合、ポリゴンの形に最も一致するH3セルの配列が生成される |
ある座標がポリゴンの内側にあるかどうかを正確に確認したい
| 交差(Intersection) | H3セルがポリゴンを完全にカバーするため、抜け穴が発生しない
|
| 包含(Containment) | H3セルがポリゴンからはみ出ることはない
|
上記の表からわかるように、1つのユースケースに対して複数のインデックス方法が適している場合があります。
さまざまな組み合わせを試して、自分のユースケースに最適なものを見つけましょう。
よし、ポリゴンのインデックスができた!どうやって使うんだっけ?
これまでにポリゴンのインデックス作成方法をいくつか解説してきましたが、具体的な使い方の例はあまり触れませんでした。
出前館ではさまざまな形で使用していますが、特に興味深いのは上記に登場したpoint-in-polygon check(多角形の点包囲チェック)だと思うので、それを見てみましょう。
冒頭でも触れましたが、H3は空間インデックスです。つまり、空間検索を高速化する仕組みです。領域をH3インデックスに変換することで、基の空間データを直接確認せずに領域を調べることができます。
具体的な例を挙げると、ある座標を包含しているポリゴンを調べたいとします。
- 説明が複雑になり過ぎないように、地球全体を網羅していて、お互いに重ならないポリゴンを持っているという前提にします。
システムにあるポリゴンを全部確認するのはかなり非効率的です。そこで、まず候補になり得るポリゴンを取得すると良いでしょう。ここはH3の出番です。
座標をH3インデックスに変換し、そのインデックスを持つポリゴンをデータベースなどでクエリします。
そして、候補のポリゴンを取得してから、本当にポリゴンに包含されているかどうかを確認するという流れになります。
簡単な図にしますと:
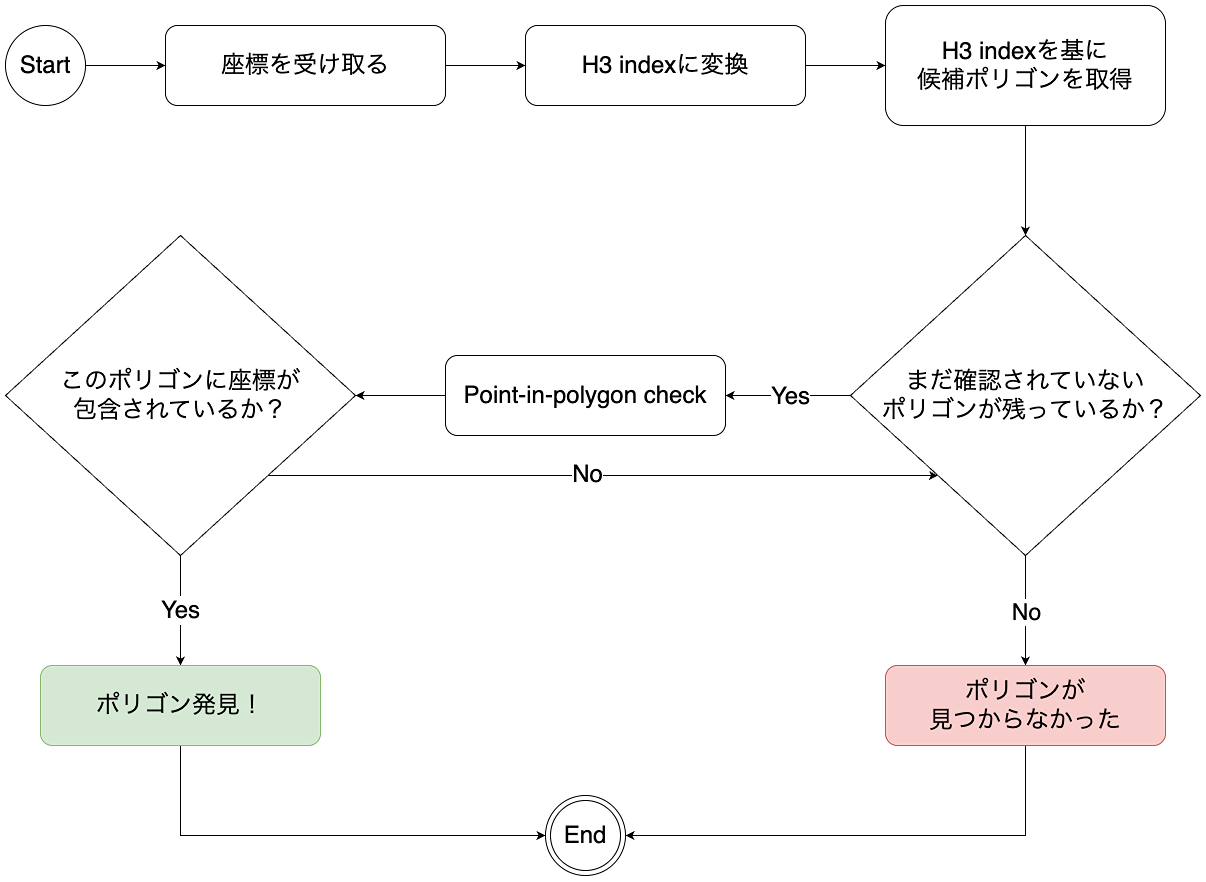
このフローで実装できますが、問題点が1つあります:point-in-polygonチェックは非効率的です。
- 代表的なアルゴリズムだと、時間計算量はO(n)になります(nはポリゴンの頂点や辺の数)
ポリゴンが簡単な形状の場合は問題ないかもしれませんが、より効率化する方法はないでしょうか?
- よく考えてみると、ポリゴンのインデックスとなっているH3セルをすべて確認する必要がないかもしれません。
インデックスのH3セルは完全にポリゴンに包含されていれば、ポリゴンの境界線からはみ出ることはありません。
つまり、point-in-polygonチェックを実行しなくても良いです。 Point-in-polygonチェックは、H3セルがポリゴンの境界線に交差している場合のみ必要です。
ポリゴンに包含されているのか、境界線に交差しているのか、といった情報をインデックスのH3セルに持たせることで、point-in-polygonチェックの回数を大幅に削減できるはずです。
- どの程度減らせるかはH3の解像度やポリゴンの形などによります。
この最適化されたフローを図にしますと:
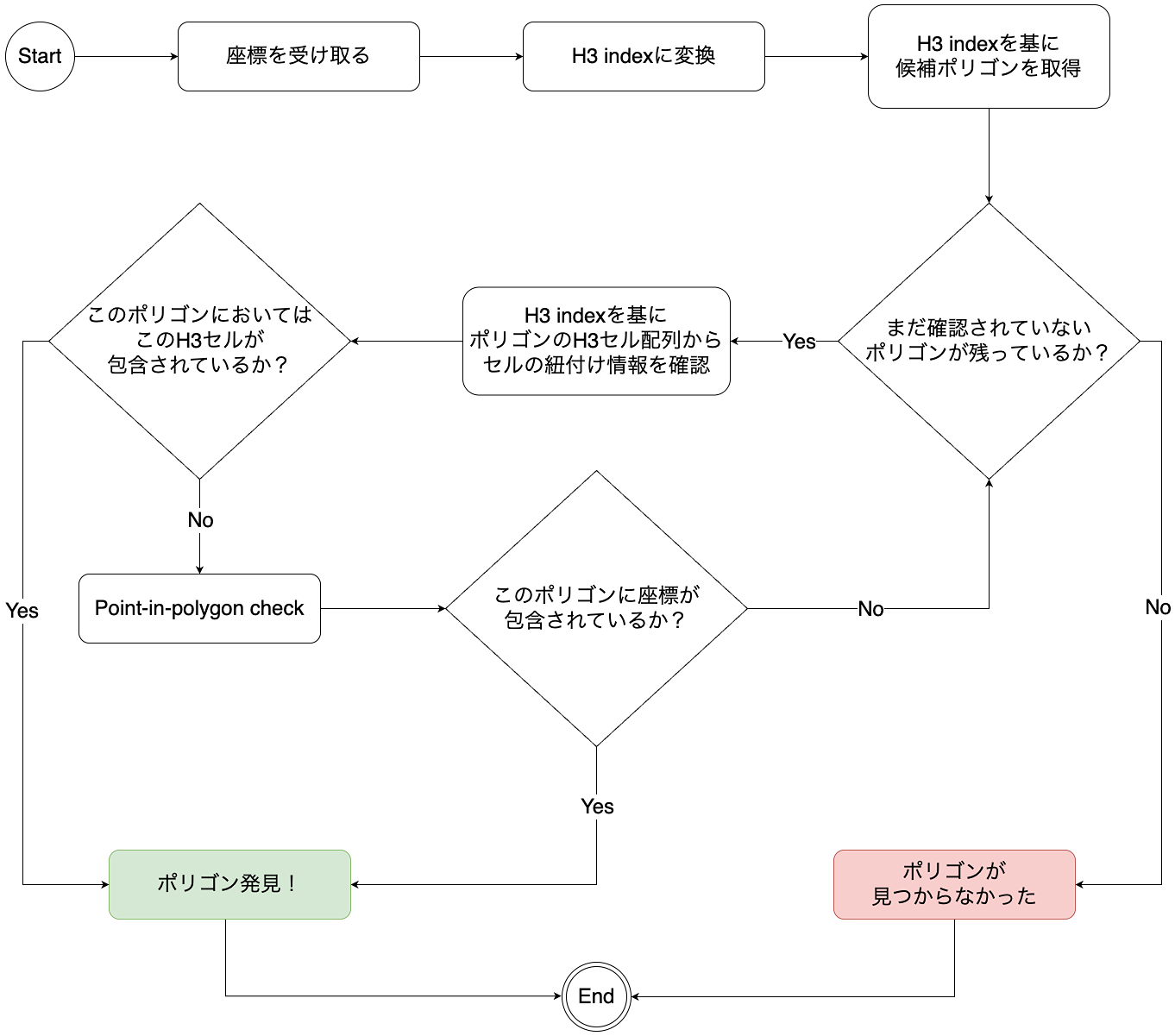
2つのインデックス方法を採用することで、より効率的なソリューションが実現できます。
フローチャートだけではイメージがなかなか湧いてこないかもしれませんので、ぜひ下記の画像をご覧ください:
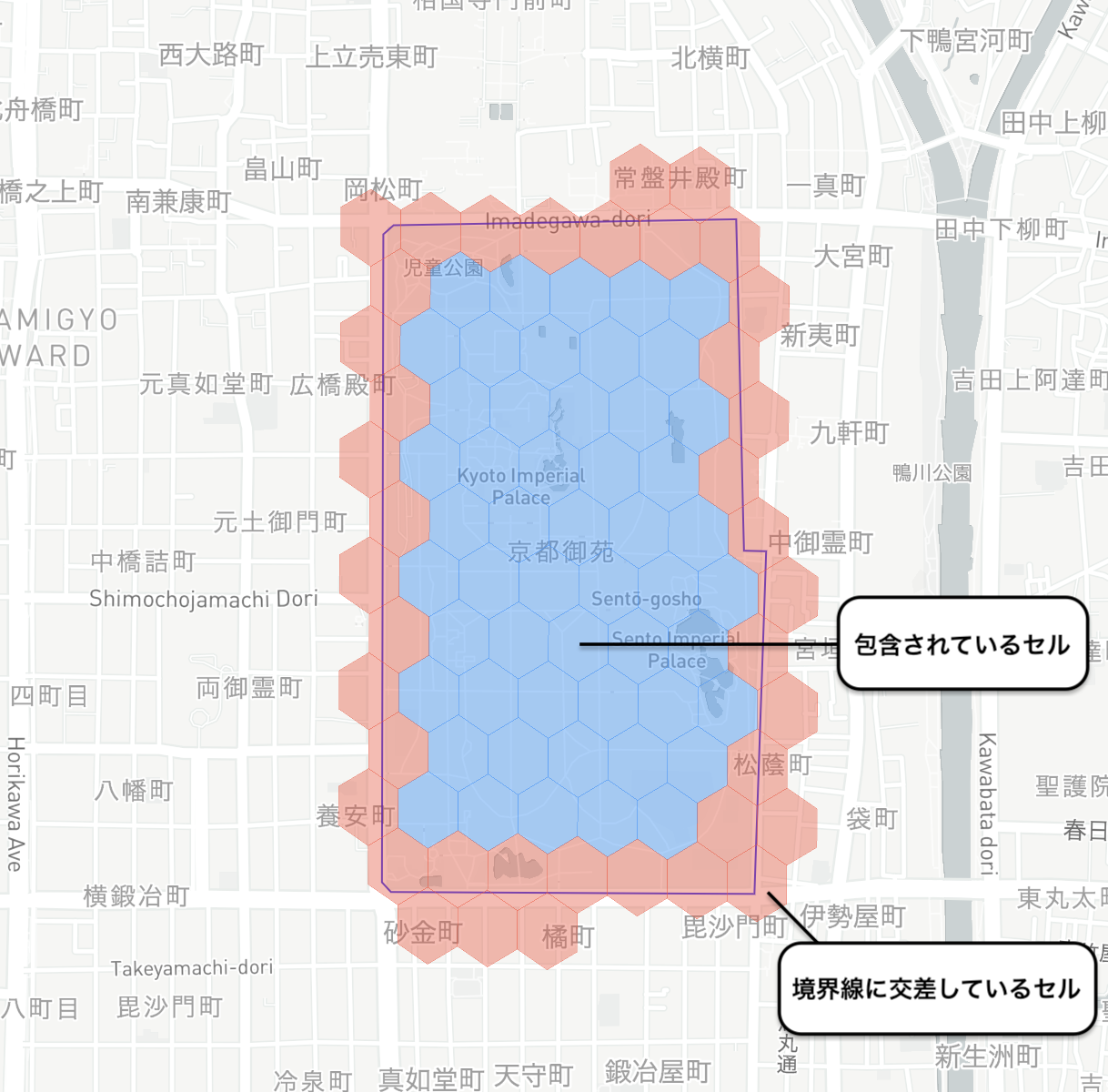
赤いH3セルはポリゴンの境界線に交差しているもので、検索の座標がその1つに該当している場合はpoint-in-polygonチェックを実行する必要があります。
H3セルがポリゴンに包含されている場合(青いセル)は、チェックを実行しなくても良いということです。
おわりに
今回はH3を利用してポリゴンを空間的にインデックスする方法を3つ紹介しました:
- 中心点:H3のデフォルト方式で、H3セルの中心点による判断
- 交差:ポリゴンに交差しているH3セルをすべて含む
- 包含:ポリゴンが完全に包含しているH3セルを含む
各アルゴリズムにはそれぞれメリットとデメリットがあるので、自分のユースケースに最適なもの(複数でもあり!)を選びましょう。
最後にH3を使用して特定の座標がどのポリゴンに包含されているかを調べるという具体的な使用例を解説しました。
また、交差と包含の2つのアルゴリズムを用いてポリゴンをインデックスすることによって、計算量の高いpoint-in-polygon check(多角形の点包囲チェック)を最適化する方法も紹介しました。
本記事に登場したアルゴリズムやテクニックを試せるObservableノートブックも用意しましたので、興味のある方はぜひご覧ください。
最後までお読みいただきありがとうございました!