はじめに
本記事では、AI 事業本部のミライネージというプロダクトで働いているデータサイエンティストが扱っている技術について紹介します。
ミライネージとはサイネージ広告を扱っているプロダクトで、全国の店舗に多数設置されているサイネージ上で広告を配信することができるシステムを提供しています。
広告配信プロダクトにおいてデータサイエンティストが果たすべき役割はいくつかあるのですが、今回は「広告配信最適化」の機能開発に関わる技術に注目して紹介していきたいと思います。
サイネージ広告では、いつ、どこのサイネージにどの広告を出すかという選択が非常に重要な要素です。すなわち、広告配信によって得られる効果が最大化されるように、適切な場所やタイミングで広告を出すことがシステムには求められています。一方で、広告主の予算や広告枠として提供されている在庫の量など、考慮しなくてはならない制約条件が存在します。
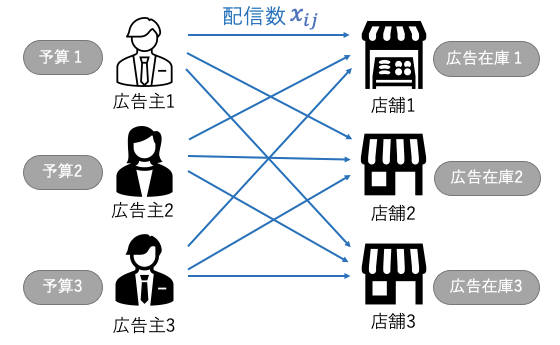
このような問題を数式で表現することで、いわゆる「数理最適化」という問題に帰着することができます。数理最適化問題とは、与えられた制約条件のもとで目的関数を最大化、あるいは最小化するような解を求める問題です。広告配信最適化の場合は、次のような問題設定をすることで数理最適化の枠組みで扱うことができることがわかります。
- 変数:各広告枠における広告の表示回数
- 制約条件:広告主の予算や広告枠の在庫量など
- 目的関数:広告効果の大きさを表すスコア
以下では、数理最適化問題の簡単な例を挙げて、問題を解く際に利用できるライブラリをいくつか紹介していきたいと思います。
数理最適化問題の具体例
数理最適化のイメージを掴むために、具体例を挙げてみましょう。
実際の広告配信最適化では多数の広告や広告枠を考慮する必要がありますが、今回は分かりやすくするために、広告 A と広告 B の 2 種類の広告の最適化問題を扱うことにします。次のような条件で広告の表示回数を最適化する問題を考えてみてください。
- 300 秒の間に広告 A または広告 B を表示させる。
- 30 秒の広告 A の表示回数を x_A、15 秒の広告 B の表示回数を x_B とする。
- 広告を 1 回表示するごとに、広告 A は 50 円、広告 B は 30 円だけ予算を消費する。
- 広告主は全部で 400 円の予算を持っている。
- 広告 A を表示した場合のスコアは 5.0、広告 B を表示した場合のスコアは 3.0 とする。
- スコアが最大となるような x_A と x_B の組合せを知りたい。
上記の条件を表にまとめると以下のようになります。
| 秒数 | 広告単価 | スコア | |
| 広告 A | 30 秒 | 40 円 | 5.0 |
| 広告 B | 15 秒 | 30 円 | 3.0 |
| 合計 | ≦ 300 秒 | ≦ 500円 |
この問題は、広告の合計秒数と予算の制約条件のもとで、スコアの最大化を目的とする数理最適化問題となっています。
この問題の制約条件を数式で表すと、次のように書くことができます。
- 30 x_A + 15 x_B \le 300
- 40 x_A + 30 x_B \le 500
これらの制約条件のもとで、最大化するべき目的関数は以下で与えられます。
- 5.0 x_A + 3.0 x_B
問題を定式化することで、数学的な計算で解を求めることができるようになりました。この問題の制約条件は、次のように図示することができます。
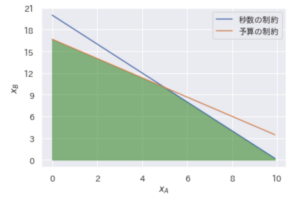
塗りつぶされた緑の範囲の中にある整数の組 x_A と x_B のうち、スコアが最大となるものを見つけることがこの最適化問題の目的となります。
数理最適化ツール
上記のような形で定式化された最適化問題を解く方法はいくつもありますが、以下では比較的簡単に利用することができる数理最適化ツールを紹介します。
PuLP
Python で整数最適化問題を記述するためのツールはいくつかありますが、まずは PuLP というライブラリを紹介します。
PuLP は COIN-OR というプロジェクトで開発されたライブラリで、数理最適化のモデリングとソルバーの呼び出しを簡単に行うことができます。ソルバーとしては無償のものや有償のものなど色々と選んで使うことができます。CBC (COIN-OR Branch and Cut) という無償のソルバーも付属しているので、容易に導入することができるでしょう。このソルバーでは、分枝限定法と切除平面法を組み合わせた分枝カット法と呼ばれるアルゴリズムで最適化問題を解いているようです。
PuLP を使って前節の最適化問題を計算する場合、以下のようなコードを記述することになります。
from pulp import *
m = LpProblem(sense=LpMaximize)
x_a = LpVariable("x_a", lowBound=0, cat="Integer") # 広告Aの表示回数
x_b = LpVariable("x_b", lowBound=0, cat="Integer") # 広告Bの表示回数
m += 5.0 * x_a + 3.0 * x_b # 目的関数(合計スコア)
m += 30 * x_a + 15 * x_b <= 300 # 秒数の制約条件
m += 40 * x_a + 30 * x_b <= 500 # 予算の制約条件
m.solve() # 最適化計算の実行
print(value(x_a), value(x_b)) # 最適化結果の出力
直感的にわかりやすい記述方法なので、内容について詳しく説明しなくても雰囲気は伝わるのではないでしょうか。このコードを実行すると、最適化問題の解である x_A = 5 と x_B = 10 を求めることができます。
Python-MIP
もうひとつ、PuLP と記法はほとんど同じなのですが、処理の高速化が行われている COIN-OR 製のライブラリとして Python-MIP というものがあります。
特に、Python-MIP では Python の CFFI モジュールを用いてソルバーとのやり取りを行うことで高速な処理を実現しているようです。Python-MIP でもソルバーとしては CBC が利用可能となっています。Python-MIP を用いた最適化計算の実装は以下のようになります。
from mip import *
m = Model()
x_a = m.add_var("x_a", var_type="I") # 広告Aの表示回数
x_b = m.add_var("x_b", var_type="I") # 広告Bの表示回数
m.objective = maximize(5.0 * x_a + 3.0 * x_b) # 目的関数(合計スコア)
m += 30 * x_a + 15 * x_b <= 300 # 秒数の制約条件
m += 40 * x_a + 30 * x_b <= 500 # 予算の制約条件
m.optimize() # 最適化計算の実行
print(x_a.x, x_b.x) # 最適化結果の出力
こちらも簡単な記述で最適化問題の解を求めることができます。ミライネージでは、配信最適化システムの構築に Python-MIP を利用しており、ある程度の規模の問題に対しては十分に実用的な性能を持っていると思います。
量子コンピュータ
ここまでに紹介した最適化問題は非常に簡単なものでしたが、多数の選択肢の中から最適な解の組合せを見つける組合せ最適化問題は一般に解くのが非常に難しいことが知られています。組合せ最適化の難しい問題では、問題の規模が大きくなるとともに計算時間が指数的に増大する場合があり、通常の計算機を用いたアルゴリズムでは計算が手に負えない可能性があります。
そのような問題に対して有効なのではないかと期待されているのが、量子コンピュータを利用したアルゴリズムです。量子コンピュータについては以下の記事でも紹介していますので、興味のある方は読んでいただけると嬉しいです。
組合せ最適化問題の難しさは解の候補の数が多すぎることが原因なのですが、量子コンピュータでは、重ね合わせ状態と呼ばれる状態を利用することで多数の解候補を同時に扱えることが特色となっています。
量子コンピュータを用いて組合せ最適化問題を扱うための方法として、イジングモデルの紹介をします。イジングモデルは上向きと下向きの 2 種類の状態を持つスピンを変数とする統計力学のモデルで、そのエネルギーに対応する関数(ハミルトニアン)は次のような形をしています。
H = -\sum_{i=1}^nh_iZ_i – \sum_{i\lt j}J_{ij}Z_iZ_j
ここで、 n 個のスピン変数 Z_i は上向きまたは下向きそれぞれに対応して + 1 または -1 の値を取ります。解きたい問題の目的関数を再現するように h_i や J_{ij} のパラメータを決めることで、最適化問題をイジングモデルで表現することができます。このとき、エネルギーが最小となるようなスピン変数の組合せを求めることが、組合せ最適化問題の解を求めることに対応していることがわかるかと思います。
実際に量子コンピュータを用いて組合せ最適化問題を計算するにはどのような手法を用いればよいか、いくつか具体的に見てみましょう。量子コンピュータの分野で研究されているものとしては、「量子ゲート方式」と呼ばれる手法と「量子アニーリング方式」と呼ばれる手法が知られています。以下では、それぞれの方式で最適化問題を計算する手法の紹介をします。
量子ゲート方式
量子ゲート方式のコンピュータでは、量子ゲートと呼ばれる演算要素の操作によって古典コンピュータでは表すことができないような状態を作り出すことができます。量子状態のエネルギーを目的関数と考えると、その最低エネルギー状態(基底状態)を求めることで最適化問題の解が得られます。
エネルギーがより小さくなるように量子ゲートのパラメータを更新することで基底状態を求める手法は変分量子固有値法(VQE)と呼ばれ、量子古典ハイブリッドアルゴリズムの一種として知られています。特に、イジングモデルの最適化問題に VQE を適用する手法は量子近似最適化法(QAOA)と呼ばれ、量子ゲート方式のコンピュータで組合せ最適化問題を解くことができる手法として有名です。参考に、QAOA における計算過程を図示したものを挙げておきます。
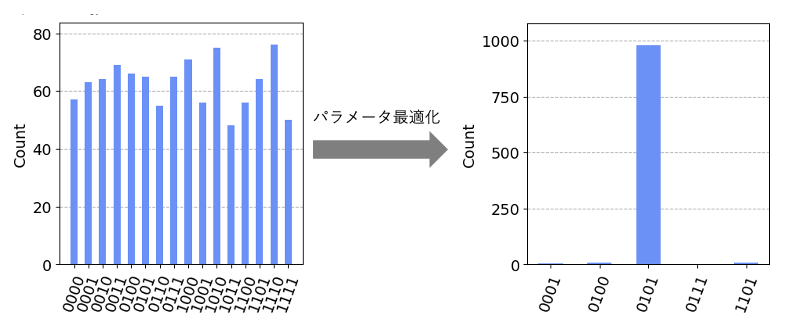
これは IBM 社が提供している qiskit というツールを用いたシミュレーションですが、量子ゲートのパラメータを調整することで基底状態を読み出すことに成功しています。シミュレーションの詳細については、以下のリンク先の実装をご確認ください。
現実の最適化問題の解法として量子ゲート方式のコンピュータが古典コンピュータを凌ぐようになるのはまだ先の話になりそうですが、盛んに研究開発が進められている分野なので今後も注目していきたいと思います。
量子アニーリング方式
量子ゲート方式のコンピュータは様々な問題への応用が考えられる汎用型の量子コンピュータですが、一方の量子アニーリング方式は組合せ最適化専用の特化型計算機となっています。
物理学の知識を応用して組合せ最適化問題を解く手法としてはシミュレーテッドアニーリングというアルゴリズムがありますが、量子アニーリングはシミュレーテッドアニーリングの量子版とでもいうような計算方法です。すなわち、シミュレーテッドアニーリングでは高温の状態から徐々に温度を下げていく過程で「熱ゆらぎ」を利用して最終的に基底状態へと導くのに対して、量子アニーリングでは「量子ゆらぎ」を利用しているという特徴があります。
量子アニーリング方式のコンピュータとしては、D-Wave 社が開発した計算機が有名です。解きたい最適化問題をこのコンピュータで計算可能なイジングモデルに対応する形で記述することで、その解を求めることができます。
また、最近では量子アニーリングの手法に影響を受けて開発された古典コンピュータの開発が国内で活発に進められています。以下に挙げるように、古典的なコンピュータを利用して組合せ最適化問題を解くことに特化したアニーリングマシンが開発されているようです。
これらの新しい手法の今後の動きにも注目していきたいところです。
まとめ
本記事では、広告配信システムを構築する上で重要となる数理最適化問題を解く際に利用できるツールの紹介を行いました。無料で利用可能な既存の数理最適化ライブラリも高性能で実用的なのですが、非常に大規模な組合せ最適化問題は従来のコンピュータでは現実的な時間で解くことができない可能性があります。そのような問題に対して、計算性能の飛躍的な向上が期待される選択肢として量子コンピュータを紹介しました。
量子コンピュータはまだ発展途上の分野で本格的な実用化には至っていませんが、注目するに値する夢のある技術だと思います。技術の発展のためには応用事例を積み重ねていくことも重要なので、ミライネージでも積極的に新しい技術の検証に取り組んでいきたいと思います。
